Cuando un cuerpo está en equilibrio, debe encontrase en reposo o en estado de movimiento rectilíneo uniforme. De acuerdo con la primera ley de Newton, lo único que puede cambiar dicha situación es la aplicación de una fuerza resultante.
sabemos que si todas las fuerzas que actúan sobre un cuerpo tienen un solo punto de intersección y si su suma vectorial es igual a cero, el sistema debe estar en equilibrio.
Cuando sobre un cuerpo actúan fuerzas que no tienen una línea de acción común, tal vez exista equilibrio traslacional pero no equilibrio rotacional.
BRAZO DE PALANCA
La distancia perpendicular del eje de rotación a la línea de acción de la fuerza se llama brazo de palanca de la fuerza, el cual determina la eficacia de una fuerza dada para provocar el movimiento rotacional.
El brazo de palanca de una fuerza es la distancia perpendicular que hay de la línea de acción de la fuerza al eje de rotación.
Debido a lo anterior, si la línea de acción de la fuerza pasa por el eje de rotación (punto A de la figura 1), el brazo de palanca es cero.
Fig 1. La fuerza no equilibrada $\textbf F$ no produce ningún efecto rotacioal
Sobre el punto A, pero cada vez es más eficaz al aumentar su brazo de palanca
Sobre el punto A, pero cada vez es más eficaz al aumentar su brazo de palanca
Si la línea de acción de la fuerza pasa por el eje de rotación (punto A de la figura 1), el brazo de palanca es cero.
Fig 2. Ejemplos de brazo de palanca
MOMENTO DE TORSIÓN
El momento de torsión $\tau$ se define como la tendencia a producir un cambio en el movimiento rotacional. Este momento también es conocido como Momento de fuerza.
Momento de torsión = fuerza X brazo de palanca
$$\tau = F\ r$$
Las unidades del momento de torsión son las unidades de fuerza por distancia, por ejemplo: newton-metro ($N \cdot m$) y libra-pie ($lb \cdot ft$)
Si la fuerza F tiende a producir una rotación contraria a la de las manecillas con respecto a
un eje, el momento de torsión se considerará positivo.
EJEMPLO 1 Se ejerce una fuerza de 250 N sobre un cable enrollado alrededor de un tambor de 120 mm de diámetro. ¿Cuál es el momento de torsión producido aproximadamente al centro del tambor?
SOLUCIÓN 2
Observa que la línea de acción de la fuerza de 250 N es perpendicular al diámetro del tambor; por lo tanto, el brazo de palanca es igual al radio del tambor.
$$r = \frac{D}{2} = \frac{120 mm}{2} = 60\ mm = 0.06m$$
Así que
$$\tau = F \cdot r = (250 N)(0.06 m) = 150 N\cdot m$$
EJEMPLO 2 Una pieza angular de hierro gira sobre un punto A, como se observa en la figura 3. Determina el momento de torsión resultante en A debido a las fuerzas de 60 N y 80 N que actúan al mismo tiempo.
Fig 3. Gráfica del ejemplo 2
SOLUCIÓN 2
Lo primero que hacemos es calcular los brazos de palanca $r_1$ y $r_2$:
$$r_1 = (12 cm)sen 50° = 9.19 cm$$$$r_2 = (10 cm)sen 70° = 9.40 cm$$
Si se considera A como eje de rotación, el momento de torsión debido a $F_1$ es negativo (sn) y el causado por $F_2$ es positivo (sp). El momento de torsión resultante se encuentra así:
$$\tau _R = \sum \tau = \tau_1 + \tau_2 + \tau _3$$$$- (60\ N)(9.19\ cm) + (80\ N)(9.40\ cm) = 200\ N \cdot cm$$
EQUILIBRIO
La condición para el equilibrio traslacional quedó establecida en forma de ecuación como
$$\sum F_x = 0\qquad \qquad \sum F_y = 0$$
Si se desea asegurar que los efectos rotacionales también estén equilibrados, es preciso estipular que no hay momento de torsión resultante. Por tanto, la segunda condición de equilibrio es:
La suma algebraica de todos los momentos de torsión respecto de cualquier
eje debe ser cero.
$$\sum \tau = \tau _1 + \tau _2 + \tau _3 + \cdots = 0 $$
EJEMPLO 3 Considere la situación que se presenta en la figura 4: Una niña que pesa 300 N y un niño que pesa 400 N están parados sobre una plataforma de 200 N de peso y sostenida por dos soportes A y B. ¿Qué fuerzas ejercen los soportes sobre la plataforma?
Fig 4
SOLUCIÓN 3
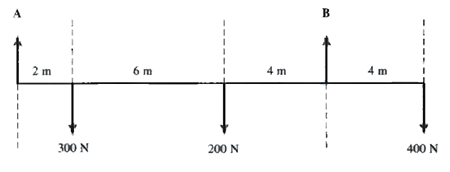
Antes de hacer cálculos, tenemos que hacer nuestro diagrama de cuerpo libre (Figura 5).
Fig 5
Aplicamos la primera condición de equilibrio a las fuerzas verticales
$$\sum F_y = 0 = A + B - 300\ N - 200\ N - 400\ N $$De donde se obtiene la ecuación
$$A + B = 900\ N$$
Esta es una ecuación con dos incógnitas y para poder resolverla es necesario más información.
Como no hay rotación, se puede seleccionar cualquier punto para considerar ahí un punto de rotación ficticio. Como la segunda condición de equilibrio involucra a las dos fuerzas, A y B, por sentido común, podemos escoger un punto donde actúe alguna de las fuerzas desconocidas con el fin de que tenga brazo de palanca cero y así desaparezca.este término en la segunda condición de equilibrio
$$\sum \tau_B = -A(12\ m) + 300\ N)(10\ m) + (200\ N)(4\ m) - (400\ m)(4\ m) = 0$$
Simplificando tenemos
$$2200\ N\cdot m = (12\ m)A$$$$\boxed {\ \ \ A = 183\ N\ \ \ }$$
Con este dato, resolvemos la primera ecuación
$$A + B = 900\ N$$$$183\ N + B = 900\ N$$$$\boxed{\ \ \ B = 771\ N \ \ \ }$$
$$A + B = 900\ N$$$$183\ N + B = 900\ N$$$$\boxed{\ \ \ B = 771\ N \ \ \ }$$
EJERCICIO 1 Una viga uniforme de 500 N de peso y 3 m de longitud está sostenida por un cable, como se observa en la figura 6. La viga se apoya en la pared y el cable forma un ángulo de 30° con respecto a la viga, que está en posición horizontal. Si una carga de 900 N se cuelga del extremo derecho,
a) ¿cuál es la tensión T del cable?
b) ¿Cuáles son las componentes horizontal y vertical de la fuerza ejercida por el pivote?
Fig 6
CENTRO DE GRAVEDAD
Cada partícula que existe en la Tierra tiene al menos una fuerza en común con cualquier otra partícula: su peso. En el caso de un cuerpo formado por múltiples partículas, estas fuerzas son esencialmente paralelas y están dirigidas hacia el centro de la Tierra. Independientemente de la forma y tamaño del cuerpo, existe un punto en el que se puede considerar que está concentrado todo el peso del cuerpo. Este punto se llama centro de gravedad del cuerpo.
EJEMPLO 4 Calcula el centro de gravedad del sistema de barra con pesas que se presenta en la figura 7. Suponga que el peso de la barra de 36 in es insignificante.
Fig 7
SOLUCIÓN 4
Como centro de gravedad es el punto donde una sola fuerza ascendente F equilibraría el sistema.
Superponiendo un diagrama de cuerpo libre en las pesas, trazamos la fuerza ascendente F en un punto localizado a una distancia desconocida x desde un punto de referencia.
Puesto que la fuerza resultante es cero, la fuerza ascendente F debe ser igual a la suma de las fuerzas hacia abajo y podemos escribir
$$F = 30\ lb + 10\ lb = 40\ lb$$
La suma de los momentos de torsión respecto al centro geométrico de la masa izquierda
también debe ser igual a cero, así que
$$\sum \tau = (40\ lb)x + 0\ lb)(0) - (10\ lb)(36\ in) = 0$$$$(40\ lb)x = 360\ lb \cdot in$$$$\boxed{\ \ \ x = 9\ in \ \ \ }$$
EJERCICIO 2 Encuentre el momento de torsión resultante respecto a la esquina A para la figura 8.
Fig 8
EJERCICIO 3 ¿Cuáles deben ser las fuerzas F¡ y F para que se alcance el equilibrio en la figura 9? No tome en cuenta el peso de la barra.
Fig 9
EJERCICIO 4 ¿Cuál es el momento de torsión resultante respecto al pivote de la figura 10? Considere que el peso de la barra curva es insignificante.
Resp. —3.42 N • m
Fig 10










No hay comentarios. :
Publicar un comentario